assuming compount interest format
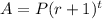
for compounded per 1 year
A=future amount
P=present amount
r=rate in decimal
t=time in years
given
P=270
r=5%=0.05
the equaton is
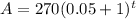
or
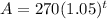
for any year, 2009, is year 0, so if you wanted to input the year then
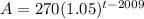
would be for t=what year it was
A.

b. 2009 to 2020
2020-2009=11 years
t=11
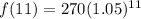
f(11)=461.792
about 462 cranes
A.

B. about 462