Answer:
First Question: C
Second Question: A
Third Question: D
Explanation:
First Question:
We need to solve the equation first and see the x and y point of the solution.
We can substitute Equation 1 into Equation 2 given, and then solve for x:
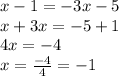
Now putting
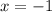 into the first equation, we get y:
into the first equation, we get y:
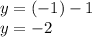
Hence, the solution is x = -1 and y = -2
Both x and y negative falls in the 3rd quadrant.
Answer choice C is right.
Second Question:
Let's solve the equation using substitution method and find the solution first.
Solving for x in Equation 1 gives us:
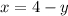
Now using this and substituting in Equation 2 we have:

Now using distributive property [
 ] and a little algebra, we solve for y:
] and a little algebra, we solve for y:

Now using value of
 and putting it in the First Equation and rearranging gives us the value of x:
and putting it in the First Equation and rearranging gives us the value of x:

So our solution is
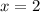 and
and

Both x and y are positive and they fall in 1st quadrant.
Choice A is right.
Third Question:
We let cost of one scarf be
 and cost of one hat be
and cost of one hat be

"The cost of four scarves and six hats is $52.00":
Cost of 4 scarves is
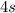 and the cost of 6 hats is
and the cost of 6 hats is

The total cost is $52, hence we can write our first equation:
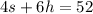
"The cost of two hats is $1.00 more than the cost of one scarf":
Cost of 2 hats is
 and cost of one scarf is
and cost of one scarf is
 , so from information given we can write second equation as:
, so from information given we can write second equation as:

We have 2 equations. Now solving for
 in second equation and putting that into first equation, we have:
in second equation and putting that into first equation, we have:
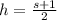
Now,
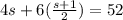
Using distributive proper [
 ] and a little algebra, we can find the value of s:
] and a little algebra, we can find the value of s:
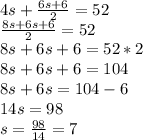
Hence, the cost of 1 scarf is $7.00
Answer choice D is right.