Answer:
Option(B) is correct.
The tenth term is given by

Explanation:
Given : The sequence 15, 13, 11, 9,....
We have to determine the equation that can be used to find the tenth term of the given sequence 15, 13, 11, 9,....
Consider the given sequence 15, 13, 11, 9,..

Difference between each term is

Since, The difference between each term is constant -2
Thus, The given sequence is an arithmetic sequence with first term 15 and common difference -2.
Thus, The general term is given by
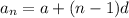
where a is first term and d is common difference nd n is number of term.
Subsitute, we have,

Simplify, we have,

Thus, The tenth term is given by
