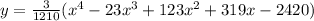Question

Find a possible formula for a fourth degree polynomial g g that has a double zero at 1 1 g(−4)=0 , g(5)=0 , and g(0)=−6

Answer 1

There's a double zero at 11, so that means (x-11)^2 is a factor

g(-4) = 0 so x+4 = 0 meaning that (x+4) is a factor
g(5) = 0 so x-5 = 0 meaning that (x-5) is a factor

all together, we have

(x-5)*(x+4)*(x-11)^2

let's expand this out

(x-5)*(x+4)*(x-11)^2
(x^2-x-20)*(x^2-22x+121)
x^2(x^2-22x+121) - x(x^2-22x+121) - 20(x^2-22x+121)
x^4-22x^3+121x^2-x^3+22x^2-121x-20x^2+440x-2420
x^4-23x^3+123x^2+319x-2420

This is multiplied by some constant k such that

k*(x^4-23x^3+123x^2+319x-2420) = -6

where plugging in x = 0 leads to -6

Let's plug in x = 0 and find out what happens with k

k*(x^4-23x^3+123x^2+319x-2420)
k*(0^4-23*0^3+123*0^2+319*0-2420)
k*(-2420)
-2420k

So -2420k = -6 leads to k = 3/1210

Therefore, the equation is
`y = (3)/(1210)(x^4-23x^3+123x^2+319x-2420)`