Please help me understand how to do this! In ΔRST shown below, segment SU is an altitude: What property or definition is needed to prove that ΔRUS is similar to ΔSUT?

Question

asked May 12, 2017 65.8k views

2 Answers

Sam Rockett · Answer 1 · 2017-05-18T16:35:34+0000

Answer:

The correct option is 1.

Explanation:

It is given that in ΔRST , segment SU is an altitude. It means the angle SUR and angle SUT are right angles.

It triangle RST and SUT,

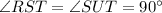$\angle RST=\angle SUT=90^(\circ)$ (Definition of altitude)

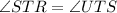$\angle STR=\angle UTS$ (Common angle)

Two corresponding angles are equal. So by AA property of similarity,

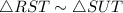$\triangle RST\sim \triangle SUT$ .... (1)

It triangle RST and RUS,

$\angle RST=\angle SUR=90^(\circ)$ (Definition of altitude)

$\angle SRT=\angle URS$ (Common angle)

Two corresponding angles are equal. So by AA property of similarity,

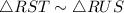$\triangle RST\sim \triangle RUS$ .... (2)

According to transitive property of equality,

if a=b and b=c, then a=c.

From (1) and (2), we get

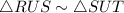$\triangle RUS\sim \triangle SUT$ ( Transitive property of equality)

Therefore the correct option is 1.