Answer:
2) x = 0.3281
3) x = 1.31
Explanation:
2. We have been given the equation
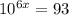
Take logarithm both sides

Use the power rule of logarithm:
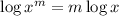
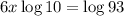
The value of log10 is 1. Hence, we have
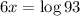
Divide both sides by 6
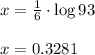
Thus the value of x is 0.3281
3)
We have to solve the equation
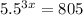 by graphing calculator.
by graphing calculator.
We graph the below two equations in the same xy- plane and the x- coordinate of the intersection point would be the solution to the graph.
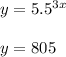
Please see the attache graph. The intersection point is (1.308,805)
The x-coordinate is 1.308. Hence, the solution is x = 1.308.
Rounded to the nearest hundredth, we have
x = 1.31