Question

What is the solution set of the quadratic inequality 6x2+1<0

Answer 1

minus 1 from both sides
6x^2<-1
divide both sides by 6
x^2<-1/6
take the square root of both sides
x<√(-1/6)
x<i√(1/6)

the solution is i√(1/6)
if you only consider real number, the solution set is empty

Answer 2

Solution set of the quadratic equation is, Empty set

Explanation:

Given the quadratic equation:
`6x^2+1>0`

Subtraction property of equality states that you subtract the same number to both sides of an equation.

Subtract both sides by 1 we get;

`6x^2+1-1>0-1`

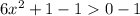
Simplify:

`6x^2>-1`

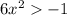
Division property of equality states that you divide the same number to both sides of an equation.

Divide both sides by 6 we get;

`(6x^2)/(6) >(-1)/(6)`

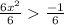
Simplify:

`x^2>(-1)/(6)`

For any x in real number there does not exist any number x which satisfy

`x^2>(-1)/(6)` , therefore, there is no solution for this set of the quadratic inequality or in other word we can say that set of the solution is Empty set.