Answer: g(x) > h(x) for x = -1.
For positive values of x, g(x) > h(x).
For negative values of x, g(x) > h(x).
Explanation:
Given functions:
 and
and
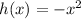
When x=0,
 and
and
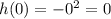
∴ at x=0, g(x)=h(0)
Therefore the statements "For any value of x, g(x) will always be greater than h(x)." and "For any value of x, h(x) will always be greater than g(x)." are not true.
When x=-1,
 and
and

∴g(x) > h(x) for x = -1. ......................(1)
When x=3,
 and
and

∴ g(x) > h(x) for x = 3....................(2)
⇒g(x) < h(x) for x = 3. is not true.
From (1) and (2),
For positive values of x, g(x) > h(x).
For negative values of x, g(x) > h(x).