Question

Point R has coordinates (1,3) and point S has coordinates (6,y). If the distances from R to S is 13 units, what are the possible values of y?

Answer 1

Answer: The required possible value of y are 15 and -9.

Step-by-step explanation: Given that the point R has co-ordinates (1,3) and point S has coordinates (6,y). Also, the distance from R to S is 13 units.

We are to find the possible values of y.

Distance formula : The distance between the points (a, b) and (c, d) is given by

`d=√((c-a)^2+(d-b)^2).`

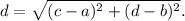
Therefore, we get

`√((6-1)^2+(y-3)^2)=13\\\\\Rightarrow 25+(y-3)^2=169~~~~~~~~~~~~[\textup{Squaring both sides}]\\\\\Rightarrow (y-3)^2=169-25\\\\\Rightarrow (y-3)^2=144\\\\\Rightarrow y-3=\pm12~~~~~~~~~~~~~~~~~~~[\textup{Taking square root on both sides}]\\\\\Rightarrow y=12+3,~~-12+3\\\\\Rightarrow y=15,-9.`

Thus, the required possible value of y are 15 and -9.

Answer 2

I tried graphing the points, and I formed a right triangle.

short leg = 6-1 = 5
Hypotenuse = 13
long leg = ?

a² + b² = c²
a² + 5² = 13²
a² = 13² - 5²
a² = 169 - 25
a² = 144
√a² = √144
a = 12

S has coordinates (6,y) = y = 12 + 3 = 15
S (6,15)