Question

What is the area of triangle ABC if AB is tangent to the circle?

Answer 1

we can use 30-60-90 triangle identity we know that since angle CBA is 30° and side AC=3, then side AB=3\sqrt{3}. There for the area is (3*3\sqrt3})/2=(9\sqrt{3})/2

Answer 2

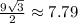`(9√(3))/(2)\approx 7.79` square units.

Explanation:

We have been given that AB is tangent to circle C. We are asked to find the area of triangle ABC.

We know that tangent is perpendicular to radius of circle, therefore, measure of angle A is 90 degrees.

Our given triangle is 30-60-90 triangle, so length of side AB (opposite to 60 degree) will be
`3√(3)`.

`\text{Area of triangle}=(1)/(2)(\text{Base*Height})`

`\text{Area of triangle}=(1)/(2)(3√(3)*3)`

`\text{Area of triangle}=(1)/(2)(9√(3))`

`\text{Area of triangle}=(9√(3))/(2)`

`\text{Area of triangle}=(1)/(2)(15.588457)`

`\text{Area of triangle}\approx 7.79`

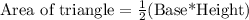
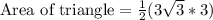
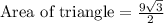
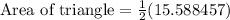
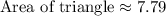
Therefore, the area of the triangle is
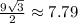`(9√(3))/(2)\approx 7.79` square units.