f(x)=
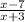
g(x)=
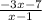
1. f(g(x))=x
f(g(x)) means to put g(x) wherever you find x in f(x).
f(g(x)) =
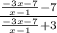
f(g(x)) =
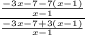
Reverse the dominator and simplify with x-1
f(g(x)) =
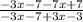
f(g(x)) =
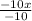
= x
So we proved that f(g(x))=x
2. g(f(x))=x
g(f(x)) means
to put f(x) wherever you find x in g(x).
g(f(x)) =
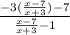
g(f(x)) =

g(f(x)) =

Reverse the dominator and simplify with x+3
g(f(x))=
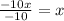
So we proved that g(f(x))=x
Because f(g(x)) = x and g(f(x)) = x f and g are inverse.