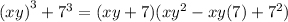Question

How would the sum of cubes formula be used to factor x3y3 + 343? Explain the process. Do not write the factorization.

Answer 1

To factor, first identify the quantities that are being cubed. The first term is the cube of xy, and the constant is the cube of 7. Next, use the formula to write the factors. The first factor is the sum of xy and 7. The second factor has three terms: the square of xy, the negative of 7xy, and the square of 7.

Explanation:

Answer 2

Given : Expression -
`x^3y^3+343`

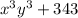
To find : How would the sum of cubes formula be used to factor given expression? Explain the process. Do not write the factorization.

Solution :

The formula of sum of cubes is,

`a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)`

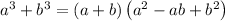
First we convert the given expression in
`a^3+b^3`

`x^3y^3+343`

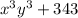
Apply exponent rule :
`a^mb^m=(ab)^m`

`x^3y^3=(xy)^3`

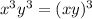
Rewrite
`343=7^3`

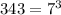
Therefore,
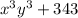`x^3y^3+343` could be written as
`=\left(xy\right)^3+7^3`

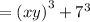
On comparison with the formula,

a=xy , b=7

`\left(xy\right)^3+7^3=(xy+7)(xy^2-xy(7)+7^2)`

`\left(xy\right)^3+7^3=(xy+7)((xy)^2-7xy+49)`