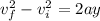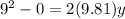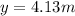Question

A mountain climber jumps a 1.9-m-wide crevasse by leaping horizontally with a speed of 9.0 m/s.. If the climber's direction of motion on landing is −45°, what is the height difference between the two sides of the crevasse?

Answer 1

y = 4.13 m

Step-by-step explanation:

Since the climber jumps horizontally with speed 9 m/s

so the time taken by the climber to cross the distance is given as

`t = (d_x)/(v_x)`

`t = (1.9)/(9)`

`t = 0.211 s`

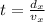
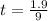
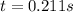
now we know that he land with a velocity at an angle of 45 degree

so we will have

`v_y = v_x`

`v_y = 9 m/s`

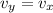
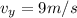
so we can find the vertical displacement by using kinematics

`v_f^2 - v_i^2 = 2 a y`

`9^2 - 0 = 2(9.81) y`

`y = 4.13 m`

Answer 2

The x component of velocity is 9.0m/s, y component is zero initially.a = -9.8m/s2
Since the jumper lands at a -45-degree angle the final Vy must have the same magnitude as the final Vx. Vf2 = V02 + 2adPlugging in values:(−9.0m/s)2=0m/s+2(−9.8m/s2)dThe height difference,d is equal to |-4.13| or 4.13 m.