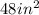Answer:
The area of the original rectangle is
Explanation:
Let's define the following variables :
 : ''Width''
: ''Width''
 : ''Length''
: ''Length''
We know that the area of the original rectangle is :
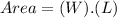
We need to find the values of this variables in order to calculate the original area of the rectangle.
We know that if the width is decreased by 3 inches, then the area of the resulting rectangle is
 . We can write the following equation :
. We can write the following equation :
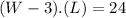 (I)
(I)
We know that the width and the length are consecutive even integers.
Therefore we have two cases :
 (A)
(A)
 (B)
(B)
Let's suppose the case (A). So if we replace the equation of the case (A) in (I) we will obtain :
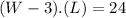
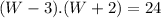
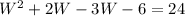
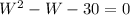
If we use the quadratic formula we will obtain two possibles values for
 :
:
 and
and
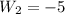
 is absurd because a length can't be negative. The value
is absurd because a length can't be negative. The value
 is possible.
is possible.
If
 , then using the equation of the case (A), we obtain that
, then using the equation of the case (A), we obtain that
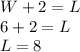
The pair :

is a possible solution for the problem. If we use the equation of the case (B) in (I) we will obtain the following expression :

If we use the quadratic formula in this equation we will obtain that
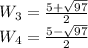
This expressions are absurd because
 must be an even integer number.
must be an even integer number.
Finally, the solution
 ,
,
 is the only correct solution.
is the only correct solution.
Calculating the area of the original rectangle :

The area of the original rectangle is