Question

A TV antenna is braced on two sides with 20-foot lengths of wire, forming an isosceles triangle with side lengths of 20 ft. If the base of the triangle is 24 ft, how tall is the antenna?

Answer 1

The height of the antenna is 16 feet.

Step-by-step explanation:

To find the height of the antenna, we can use the Pythagorean theorem.

Let's call the height of the antenna 'h'.

Since the triangle is isosceles, the two sides opposite the equal angles are congruent.

Therefore, the two sides of length 20 ft are equal to each other.

Using the Pythagorean theorem, we can set up the equation:

`h^2 + (12)^2 = 20^2.`

Simplifying, we get:
`h^2 + 144 = 400.`

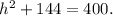
Rearranging the equation, we have:
`h^2 = 400 - 144`

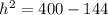
= 256.

Taking the square root of both sides, we find h = 16 ft.

Therefore, the antenna is 16 feet tall.

Answer 2

the height of the antenna is 16 ft.

Step-by-step explanation:

Given three sides of the triangles as, 20ft, 20ft, amd 24 ft.

Apply Heroes' formula to determine the area of the triangle;

`s = (20 + 20 + 24)/(2) \\\\s = 32\\\\Area = √(s(s-20)(s-20)(s-24)) \\\\Area = √(32(32-20)(32-20)(32-24)) \\\\Area = 192 \ ft^2`

The area of the triangle is also calculated as;

`Area = (1)/(2) * \ base \ * \ height\\\\A= (1)/(2) bh\\\\2A = bh\\\\h = (2A)/(b) \\\\h = (2* 192)/(24) \\\\h = 16 \ ft`

Therefore, the height of the antenna is 16 ft.