Question

Verify the basic identity. What is the domain of validity? cot theta = cos theta csc theta

Answer 1

The domain of validity of the given identity is:

• All real numbers except nπ where n belongs to integers.

Explanation:

We are asked to prove the trignometric identity:

`\cot \theta=\cos \theta\csc \theta`

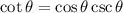
We know that:

`\cot \theta=(\cos \theta)/(\sin \theta)`

Hence, the function cotangent is defined where the denominator is not zero i.e. all the real numbers except where sine function is zero.

We know that the zeros of sine function are of the type: nπ where n belongs to integers.

Also, we can write the expression by:

`\cot \theta=\cos \theta\cdot (1)/(\sin \theta)`

We know that cosecant function is the reciprocal of the sine function.

i.e.

`\csc \theta=(1)/(\sin \theta)`

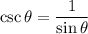
Hence, we get:

`\cot \theta=\cos \theta\cdot \csc \theta`

Answer 2

Both sides can be the domain of validity since both are just simple but what we are going to change is the right side.
Let us review that
`cot \alpha = (cos \alpha )/(sin \alpha )` and
`csc \alpha = (1)/(sin \alpha )`.
So, to prove the following identity:

`cot \alpha =cos \alpha csc \alpha`
Let us substitute the value of csc with respect to sin.

`cot \alpha =cos \alpha * (1)/(sin \alpha )`

`cot \alpha = (cos \alpha )/(sin \alpha )`

`cot \alpha =cot \alpha`