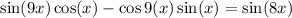Question

Write the expression as the sine, cosine, or tangent of an angle.
sin 9x cos x - cos 9x sin x

Answer 1

from sin(a-b) = sin(a)cos(b) - cos(a)sin(b)
let a=9x, b=x
sin(9x)cos(x) - cos(9x)sin(x) = sin(9x-x) = sin(8x)

Answer 2

`\sin (9x)\cos (x) - \cos 9(x) \sin (x)=\sin (8x)`

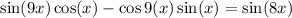
Explanation:

Given : Expression
`\sin (9x)\cos (x) - \cos 9(x) \sin (x)`

To find : Write the expression as the sine, cosine, or tangent of an angle?

Solution :

We know the trigonometry property of additional,

`\sin A\cos B-\cos A\sin B=\sin (A-B)`

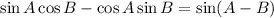
On comparing the expression with property,

A=9x and B=x

Substitute in formula,

`\sin (9x)\cos (x) - \cos 9(x) \sin (x)=\sin (9x-x)`

`\sin (9x)\cos (x) - \cos 9(x) \sin (x)=\sin (8x)`

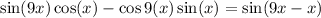
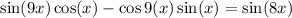
Therefore, The expression is written as the sine of an angle

`\sin (9x)\cos (x) - \cos 9(x) \sin (x)=\sin (8x)`