Question

The area of the shaded segment is 100cm^2. Calculate the value of r.

Answer 1

Hello,

The formula for finding the area of a circular region is:
`A= ( \alpha *r^(2) )/(2)`

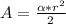
then:

`A_(1) = (80*r^(2) )/(2)`

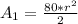
With the two radius it is formed an isosceles triangle, so, we must obtain its area, but first we obtain the height and the base.


`cos(40)= (h)/(r) \\ \\ h= r*cos(40)\\ \\ \\ sen(40)= (b)/(r) \\ \\ b=r*sen(40)`

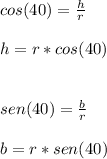
Now we can find its area:

`A_(2)=2* (b*h)/(2) \\ \\ A_(2)= [r*sen(40)][r*cos(40)]\\ \\A_(2)= r^(2)*sen(40)*cos(40)`

The subtraction of the two areas is 100cm^2, then:


`A_(1)-A_(2)=100cm^(2) \\ (40*r^(2))-(r^(2)*sen(40)*cos(40) )=100cm^(2) \\ 39.51r^(2)=100cm^(2) \\ r^(2)=2.53cm^(2) \\ r=1.59cm`

Answer: r= 1.59cm

Answer 2

Ok so we need to subtract the area of the triangle from the area of the segment and this will equal 100.
We know that the area of the segment is:

`(80)/(360) * \pi r^(2)`
And that the area of the triangle is:

`(1)/(2) r^(2) sin(80)`
Therefore:

`(80)/(360) * \pi r^(2) - (1)/(2) r^(2) sin(80)=100`
We can simplify it through these steps:

`(80)/(360) * \pi r^(2) - (1)/(2) r^(2) sin(80)=100`

`4 \pi r^(2) - 9 r^(2) sin(80)=1800`

`r^(2)(4 \pi -9sin(80))=1800`

`r^(2) = (1800)/(4 \pi -9sin(80))`

`r= \sqrt{(1800)/(4 \pi -9sin(80)) }`
Therefore r=22.04cm (4sf)