Question

The growth of a bug population shows a geometric sequence as shown in the table. This pattern continues indefinitely. What will the population be on Week 20?

♦about 1,496,366
♦about 997,577
♦about 665,051
♦about 464,758

Answer 1

The common ratio is,
r= 450/300 = 3/2


nth term of geometric series is given by,
a
`_(n)` = a₁r
`^(n-1)`
a₂₀ = 300(3/2)¹⁹ = 665051

Answer 2

the population be on Week 20 is about 665,051

Explanation:

The growth of a bug population shows a geometric sequence as shown in the table

For all geometric sequence , there should be a common ratio

Lets find common ratio 'r'

To find common ratio we divide second term by first term

so common ratio
`r= (450)/(300) =(3)/(2)`

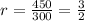
To find nth term of geometric sequence , formula is

`a_n = a_1(r)^(n-1)`

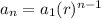
Where a1 is the first term and r is the common difference

a1= 300 and r= 3/2

We need to find the population on Week 20, so n= 20

We plug in all the values and find out a20

`a_(20) = 300((3)/(2))^(20-1)`

`a_(20) = 300((3)/(2))^(19)=300*2216.83782=665051.346`

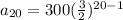
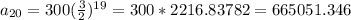
the population be on Week 20 is about 665,051