Question

For a binomial distribution with p = 0.20 and n = 100, what is the probability of obtaining a score less than or equal to x = 12? hint: use interval-based calculations because no critical region is involved.​

Answer 1

The binomial distribution is given by,
P(X=x) =
`(^(n)C_(x))p^(x) q^(n-x)`
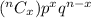
q = probability of failure = 1-0.2 = 0.8
n = 100
They have asked to find the probability of obtaining a score less than or equal to 12.
∴ P(X≤12) =
`(^(100)C_(x))(0.2)^(x) (0.8)^(100-x)`
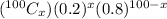
where, x = 0,1,2,3,4,5,6,7,8,9,10,11,12
∴ P(X≤12) =
`(^(100)C_(0))(0.2)^(0) (0.8)^(100-0) + (^(100)C_(1))(0.2)^(1) (0.8)^(100-1)` +
`(^(100)C_(2))(0.2)^(2) (0.8)^(100-2) + (^(100)C_(3))(0.2)^(3) (0.8)^(100-3)` +
`(^(100)C_(4))(0.2)^(4) (0.8)^(100-4) + (^(100)C_(5))(0.2)^(5) (0.8)^(100-5)` +
`(^(100)C_(6))(0.2)^(6) (0.8)^(100-6) + (^(100)C_(7))(0.2)^(7) (0.8)^(100-7)` +
`(^(100)C_(8))(0.2)^(8) (0.8)^(100-8) + (^(100)C_(9))(0.2)^(9) (0.8)^(100-9)` +
`(^(100)C_(10))(0.2)^(10) (0.8)^(100-10) + (^(100)C_(11))(0.2)^(11) (0.8)^(100-11)` +
`(^(100)C_(12))(0.2)^(12) (0.8)^(100-12)`


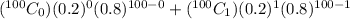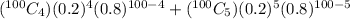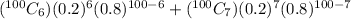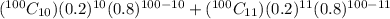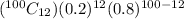
Evaluating each term and adding them you will get,
P(X≤12) = 0.02532833572
This is the required probability.