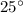Answer:
Part 1)
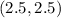 and
and
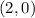
Part 2)

Part 3) m∠KLJ=
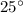
Explanation:
Part 1)
we have
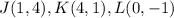
Find the coordinates of the midpoint JK
the x-coordinate of the midpoint JK is equal to
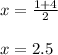
the y-coordinate of the midpoint JK is equal to
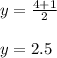
The midpoint JK is the point
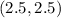
Find the coordinates of the midpoint LK
the x-coordinate of the midpoint LK is equal to
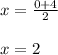
the y-coordinate of the midpoint LK is equal to
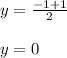
The midpoint LK is the point
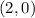
The answer part 1) is
the endpoint coordinates for the midsegment of △JKL that is parallel to JL are the points
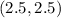 and
and
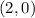
Part 2)
we know that
The diagonals bisect the parallelogram into two congruent triangles
In the parallelogram ABCD
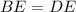
substitute the values

Solve the quadratic equation
The formula to solve a quadratic equation of the form
 is equal to
is equal to
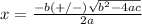
in this problem we have

so
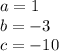
substitute in the formula
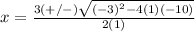
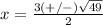
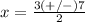
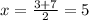

Find the value of BD

Substitute the value of

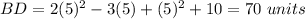
Part 3)
we know that
The diagonals bisect the parallelogram into two congruent triangles
In the parallelogram JKLM
m∠KLJ=m∠MLJ
we have that
m∠MLJ=
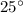
therefore
m∠KLJ=