Question

Can someone please help me on this ASAP

In the figure k>0.

(a) Is ABC PQR? Support your answer with a theorem or postulate.

(b) How does the area of PQR compare to the area of ABC? Justify your answer.

Answer 1

(a) Triangles ABC and PQR are similar triangles since they both share 2 congruent angles and therefore their 3rd angle is also congruent. So the triangles are similar due to the AAA similarity theorem. (b) The area of triangle PQR is 1 million times larger than the area of triangle ABC. This can be shown since the area of a triangle is 1/2 base times height. You can show that the base of triangle PQR is 1000 times larger than the base of triangle ABC. And since all the sides are in proportion to each other, the height of triangle PQR is also 1000 times larger than the height of triangle ABC. And since 1000 times 1000 equals 1,000,000 or 1 million, the area of triangle PQR is 1 million times larger than triangle ABC.

Answer 2

(a) Yes, Δ ABC and ΔPQR are similar triangles.

(b) Ratio of the areas of ΔPQR and ΔABC will be k².

Explanation:

In the figure attached two triangles, Δ ABC and Δ PQR have been given.

(a).In these triangle ∠ABC ≈ ∠PQR, ∠ACB ≈ ∠PRQ (Given)

Since it is given that two angles of the given triangles are equal so third angle will also be equal.

So by the theorem AAA both the triangles will be similar.

(b). Since in two similar triangles corresponding sides are in the same ratio (By theorem of similar triangles)

Therefore, sides of Δ PQR and Δ ABC will be in the same ratio = k where k > 1

Now area of Δ ABC A=
`(1)/(2)(AB)(Height)=(1)/(2)(AB)(h)`

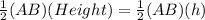
Similarly area of Δ PQR =
`A`

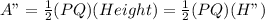
Now ratio of area of Δ PQR and Δ ABC

`(A`

`(A`

`(A`

`(A`

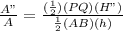
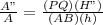
So ratio of area of Δ PQR and Δ ABC will be k².