Question

Angle $eab$ is a right angle, and $be = 9$ units. what is the number of square units in the sum of the areas of the two squares $abcd$ and $aefg$?

Answer 1

Let the measure of side AB be x, then, the measue of side AE is given by


`AE=√(9^2-x^2)`.

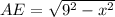
Now, ABCD is a square of size x, thus the area of square ABCD is given by


`Area=x^2`

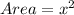
Also, AEFG is a square of size
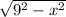
`√(9^2-x^2)`, thus, the area of square AEFG is given by


`Area=\left(√(9^2-x^2)\right)^2=9^2-x^2=81-x^2`

The sum of the areas of the two squares ABCD and AEFG is given by


`x^2+81-x^2=81`

Therefore, the number of square units in the sum of the areas of the two squares ABCD and AEFG is 81 square units.