Question

Which graph represents the solution set of the system of inequalities?

{y>_ 1/2x+1

{y>-x-2


Pleaseeee help!!!!! I will mark you as brainlinest for correct answer!!!!!

Answer 1

it is a.

Explanation:

Answer 2

Option 2nd is correct

Explanation:

To graph the given inequality, graph the boundary of these equations.

Use dashed line if < or > used to indicate that the boundary is not the part of the solution.

Use solid line if ≤ or ≥ used to indicate that the boundary is included in the solution.

Given the system of inequalities:

`y\geq (1)/(2)x+1`

`y>-x-2`

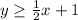
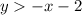
First graph the inequality
`y>-x-2`.

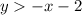The related equation is
`y=-x-2`.

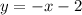Since this is strict inequality '>', so the border is dotted.

x-intercept:

Substitute value y=0 in
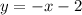`y=-x-2` to solve for x

0 = -x-2

x = -2

x-intercept = (-2, 0)

y-intercept

Substitute value x=0 in
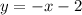`y=-x-2` to solve for y

y= 0-2

y = -2

y-intercept = (0, -2)

Since the sign of inequality is >, therefore the point on the line does not contains the solution set and shade the upper half of the line.

Now, graph the inequality
`y\geq (1)/(2)x+1` .

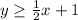The related equation is
`y=(1)/(2)x+1`

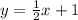
Since, this inequality is '≥' not the strict one, the border line is solid.

x-intercept:

Substitute value y=0 in
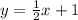`y=(1)/(2)x+1` to solve for x

`0=(1)/(2)x+1`

`-1=(1)/(2)x`

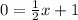
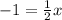
⇒x = -2

x-intercept = (-2, 0)

y-intercept

Substitute value x=0 in
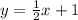`y=(1)/(2)x+1` to solve for y

`y=(1)/(2)(0)+1`

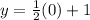
y =1

y-intercept = (0, 1)

Since the sign of inequality is ≥ , therefore the point on this line contain in the solution set and shade the upper half of the line.

You can see the graph of these system of inequalities.