Answer: X-rays are found in the given region.
Step-by-step explanation:
To calculate the wavelength of light, we use the equation:
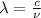
where,
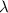 = wavelength of the light
= wavelength of the light
c = speed of light =
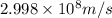
 = frequency of light =
= frequency of light =

From above, we know that frequency is inversely related to wavelength of light. Thus, the region having frequency more than the given one will have wavelength less than the calculated one.
Putting the values in above equation, we get:

(Conversion factor:
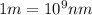 )
)
The region where wavelength is less than
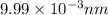 is X-rays.
is X-rays.
Hence, X-rays are found in the given region.