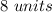Question

What is the length of the midsegment of this trapezoid?

Enter your answer in the box.

Answer 1

I believe it is 8 because
`EF= (AB+CD)/(2) = EF= (5+11)/(2) =8`

Answer 2

we know that

The midsegment of a trapezoid is the segment connecting the midpoints of the two non-parallel sides of the trapezoid, and is parallel to the pair of parallel sides.

In this problem

the two non-parallel sides of the trapezoid are AD and BC

Step 1

Find the midpoint side AD

Let

E-------> the midpoint AD

`A(2,4)\ D(-2,-1)`

Find the x-coordinate of the midpoint AD

`x=(2-2)/(2)=0`

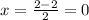
Find the y-coordinate of the midpoint AD

`y=(4-1)/(2)=1.5`

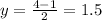
the point E is equal to
`(0,1.5)`

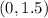
Step 2

Find the midpoint side BC

Let

F-------> the midpoint BC

`B(7,4)\ C(9,-1)`

Find the x-coordinate of the midpoint BC

`x=(9+7)/(2)=8`

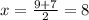
Find the y-coordinate of the midpoint BC

`y=(4-1)/(2)=1.5`

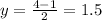
the point F is equal to
`(8,1.5)`

Step 3

Find the distance EF

we know that

The formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

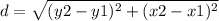
we have

`E(0,1.5)\ F(8,1.5)`

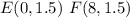
substitute the values

`d=\sqrt{(1.5-1.5)^(2)+(8-0)^(2)}`

`d=8\ units`

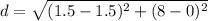
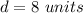
therefore

the answer is

the length of the midsegment of the trapezoid is
`8\ units`