Question

​ AD¯¯¯¯¯ ​, BD¯¯¯¯¯ , and CD¯¯¯¯¯ are angle bisectors of the sides of △ABC . AG=5 m and AD=13 m. What is DF ? Enter your answer in the box. m Note: Image may not be drawn to scale. Triangle A B C with three dashed rays drawn that intersect at point D. Ray C D intersects side A B. Ray B D intersects side A C. Ray A D intersects side B C. Three line segments extend from point D. Segment DE is perpendicular to side A B. Segment F D is perpendicular to side B C. Segment G D is perpendicular to side A C.

Answer 1

The correct answer is
DF = 12m

Answer 2

The length of DF is 12 m.

Explanation:

From the given description we can draw a figure as shown below. The lines AD,BD and CD are bisectors. The sides DE,DF and DG are perpendicular to AB,BC and CD respectively.

Draw a circle inside the triangle ABC centered at D. Since the sides DE,DF and DG are perpendicular to AB,BC and CD respectively, therefore the lines DE,DF and DG are radius of the circle.

Use pythagoras is triangle ADG.

`hypotenuse^2=base^2+perpendicular^2`

`AD^2=AG^2+DG^2`

`13^2=5^2+DG^2`

`169=25+DG^2`

`144=DG^2`

`12=DG`

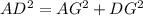
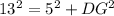
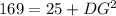
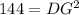
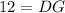
The length of DG is 12, therefore the radius of the circle is 12.

Since DF is the radius of the circle, therefore the value of DF is 12.