Question

HELP PLEASE: I don't understand how to transform into vertex form at all.

Convert this quadratic function to vertex form.
y=x^2+14x+48
Then determine the minimum value of the function.

Correctly completes the square to convert the function into vertex form.
Correctly determines the minimum value of the function.

Answer 1

`y(x) = x^(2) + 14x + 48`

`y = x^(2) + 14x + 49 - 49 + 48 \text{ *}`

`y = (x + 7)^(2) - 1`

`\boxed{y + 1 = (x + 7)^(2)}`

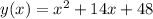
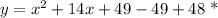
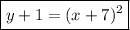
* Completing the square:
The whole premise behind 'completing the square' was to isolate the x variable by itself in the form of a quadratic function. To understand this concept, we need to look back at the whole idea that when expanding a binomial with degree 2, we will get a predictable pattern specifically:


`(x + y)^(2) = x^2+\boxed{2}xy+y^2`

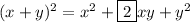
This allowed us to then create a new concept (completing the square), where we attempt to revert back to our simplest form. To understand more about the history and proof, you can search up: "Completing the square".