The number of ways n different objects can be arranged, taking r objects at a time, without repeating any object is given by:
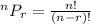
Given 6 different digits, the number of ways to arrange 6 different digits to make a 3 digit number without reapeating a digit is given by:
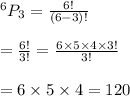
Therefore, the number of
ways 6 digits can be arranged to make a 3-digit number without repeating a digit is 120 ways.