Question

A circle is centered at the point (5, -4) and passes through the point (-3, 2).

The equation of this circle is (x +__ )^2 + (y +__ )^2 = __

Answer 1

Answer: The full equation would be (x + -5)^2 + (y + 4)^2 = 100

Step-by-step explanation: That is the correct answer on Plato/Edmentum.

Answer 2

The equation of a circle with center (a, b) and center r, is:


`\displaystyle{ (x-a)^2+(y-b)^2=r^2`.


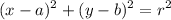
We have the center, so we can substitute a=5, and b=-4 in the equation. But we still need the radius.


The radius of a circle is the distance between the center ( (5, -4) ) and any point of the circle ( (-3, 2) ). Using the formula of the distance between 2 points, we have:


`\displaystyle{ r= √((5-(-3))^2+(-4-2)^2)= √(8^2+(-6)^2)= √(64+36)=10`.

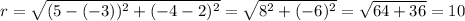
Substituting in the equation, we have:


`\displaystyle{ (x-5)^2+(y-(-4))^2=10^2`,

that is
`\displaystyle{ (x-5)^2+(y+4)^2=100`.


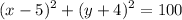
Answer: (x +_(-5)_ )^2 + (y +_4_ )^2 = _100_