Question

GIVEN: ab perpendicular to BC AND DC PERPENDICULAR TO BC

AC = BD
PROVE:AB =DC

Proofs

Answer 1

Let's take a look at the triangles ABC and DCB

1. angles : B=C=90° because they are right triangles (AB perpendicular to BC and DC perpendicular to BC)

2. AC=BD (given)
3. BC is in common (the two triangles have it, you can say it like BC=BC)

So we proved that by SAS(side angle side), the triangles are congruent ABC= DCB

Since the triangles are congrueny, all their sides are equal so we can say that AB=DC

Answer 2

Answer with Step-by-step explanation:

We are given that AB is perpendicular to BC and DC perpendicular to BC.

AC=BD

We have to prove that AB=DC

In triangle ABC and triangle DCB

AC=BD (Given)

`\angle B=\angle C=90^(\circ)`

`BC=BC`

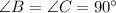
Reason:Reflexive property

`\triangle ABC\cong \triangle DCB`

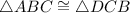
Reason:RHL postulate

`AB\cong DC`

Reason:CPCT

Therefore, AB=DC when two sides are congruent then the sides are equal.

Hence, proved.