Question

Three friends were born in consecutive years. The some of their birth years is 5982.find the year in which each person was born

Answer 1

Because the three numbers are consecutive, if the first one is x, the second should be x+1, and the third one is x+2
the three numbers add up to be 5982, so
x+(x+1)+(x+2)=5982
3x+3=5982
3x=5979
x=1993
1993,1994,1995

Answer 2

The birth years of first person is 1993.

The birth years of second person is 1994.

The birth years of third person is 1995.

Explanation:

Three friends were born in consecutive years

Let the birth years of first person be x,

Let the birth years of second person be (x+1)

Let the birth years of third person be(x+2)

The sum of their birth years is 5982.

`x+(x+1)=(x+2)=5982`

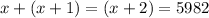
Solving the given equation for x:

`3x+3=5982`

`x=(5982-3)/(3)=1993`

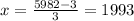
The birth years of first person = x = 1993

The birth years of second person = (x+1) = 1993+ 1 = 1994

The birth years of third person = (x+2) = 1993+2 = 1995