Question

Find the intervals of convergence for the function. f(x)=sum_(n=1)^infinity x**n/n**2 32324243232 incorrect: your answer is incorrect. (b) find the intervals of convergence for f '.

Answer 1

`\displaystyle\sum_(n\ge1)(x^n)/(n^2)`

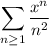
will converge as long as


`\displaystyle\lim_(n\to\infty)\left|((x^(n+1))/((n+1)^2))/((x^n)/(n^2))\right|<1`

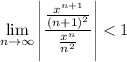
according to the ratio test. We have


`\displaystyle\lim_(n\to\infty)\left|((x^(n+1))/((n+1)^2))/((x^n)/(n^2))\right|=|x|\lim_(n\to\infty)(n^2)/((n+1)^2)=|x|\left(\lim_(n\to\infty)\frac n{n+1}\right)^2=|x|<1`

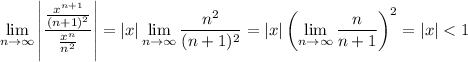
so the sum will certainly converge whenever
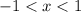
`-1<x<1`, but we also know the series will converge at the endpoints.
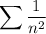
`\displaystyle\sum\frac1{n^2}` is a convergent
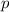
`p`-series, which means
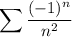
`\displaystyle\sum((-1)^n)/(n^2)` is also (absolutely) convergent, so in fact the interval of convergence is
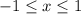
`-1\le x\le1` (endpoints included).