Question

A chess board has 64 squares. if you put one grain of rice on the first square, two grains on the second square, four grains on the third, eight grains on the fourth, and so on. how many grains are on the last square. no calculators.

Answer 1

Consider this geometric sequence.

1, 2, 4, 8, ...
By considering the ratio between the first and the second, and the second and the third, we can begin to see that it has an equal ratio of 2.

Using the geometric sequence formula:

`T_(n) = a_1 \cdot r^(n)`

`T_(n) = 1 \cdot 2^(n)`

`\text{Last square occurs when n = 64: } T_(64) = 2^(64)`

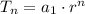
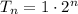
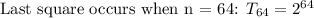
This means there will be 2^64 grains on the last square.

Answer 2

On the first square, you have 2^0 rice grains on it.
On the second, you have 2^1 rice grains on it.
On the third, you have 2^2 rice grains on it.
Repeat this pattern.
On the 64th (last square), you have 2^63 rice grains on it.
I'm not sure how you would calculate 2^63 without a calculator...
Have an awesome day! :)