Find the equation to the line that is perpendicular to y=2x-3 and goes through the point (-1,2)

Question

asked Dec 8, 2018 59.0k views

1 Answer

Flowstoneknight · Answer 1 · 2018-12-12T08:45:40+0000

first off, let's see this equation
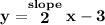
$\bf y=\stackrel{slope}{2}x-3$

so, notice, since it's already in slope-intercept form, we know the slope is just 2.

a line that is perpendicular to it, will have a negative reciprocal slope to it, let's check.

$\bf \textit{perpendicular, negative-reciprocal slope for slope}\quad 2\implies \cfrac{2}{1}\\\\ slope=\cfrac{2}{{{ 1}}}\qquad negative\implies -\cfrac{2}{{{ 1}}}\qquad reciprocal\implies - \cfrac{{{ 1}}}{2}$

so, what is the equation of a line whose slope is -1/2 and goes through -1,2?

$\bf \begin{array}{lllll} &x_1&y_1\\ % (a,b) &({{ -1}}\quad ,&{{ 2}}) \end{array} \\\\\\ % slope = m slope = {{ m}}= \cfrac{rise}{run} \implies -\cfrac{1}{2} \\\\\\ % point-slope intercept \stackrel{\textit{point-slope form}}{y-{{ y_1}}={{ m}}(x-{{ x_1}})}\implies y-2=-\cfrac{1}{2}[x-(-1)] \\\\\\ y-2=-\cfrac{1}{2}(x+1)\implies y-2=-\cfrac{1}{2}x-\cfrac{1}{2}\implies y=-\cfrac{1}{2}x-\cfrac{1}{2}+2 \\\\\\ y=-\cfrac{1}{2}x+\cfrac{3}{2}$

Find the equation to the line that is perpendicular to y=2x-3 and goes through the point (-1,2)

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

Please log in or register to add a comment.

No related questions found

Categories

Other Questions