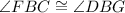FBC and CBG are supplements, DBG and DBF are supplements, and CBG DBF. By the congruent supplements theorem, what can you conclude?

Question

asked Apr 11, 2018 120k views

2 Answers

Nymk · Answer 1 · 2018-04-15T18:33:52+0000

We will use Congruent supplements theorem, which states If 2 angles are supplementary to the same angle, then they are congruent to each other.

Since, angles FBC and CBG are supplements to each other.

So,
$\angle FBC \cong \angle CBG$

Angles DBG and DBF are supplements to each other.

So,
$\angle DBG \cong \angle DBF$

And angles CBG and DBF are supplements to each other.

So,
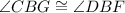
$\angle CBG \cong \angle DBF$

By using these congruent conditions, we conclude that angles FBC and DBG are congruent to each other.

Therefore,
$\angle FBC \cong \angle DBG$