Answer:
Option: A is the correct answer.
The sum is:
![4x(\sqrt[3]{2y})+12x^2y(\sqrt[3]{2y^2})](https://img.qammunity.org/2018/formulas/mathematics/high-school/viooaif6aan8k9ty2cmi4jodf6qekrrgdv.png)
Explanation:
We are given a expression as:
![2(\sqrt[3]{16x^3y})+4(\sqrt[3]{54x^6y^5})](https://img.qammunity.org/2018/formulas/mathematics/high-school/lo60hvvyfmwswsinus9f4un2psv1sdmcs6.png)
Since, the quantity which comes three times inside the cube root sign comes out as a single.
( i.e. if we have:
![\sqrt[3]{x^3}=x](https://img.qammunity.org/2018/formulas/mathematics/high-school/10gcb7y6ydem83ius4k9hq63mk0mqvsk3l.png) )
)
Also,
![2(\sqrt[3]{16x^3y})=2(2x\sqrt[3]{2y})\\\\i.e.\\\\2(\sqrt[3]{16x^3y})=4x(\sqrt[3]{2y})](https://img.qammunity.org/2018/formulas/mathematics/high-school/k6nd73ygnbdacmfcwht0vqcer0nkzv18j8.png)
( Since,
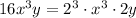 )
)
Also,
![4(\sqrt[3]{54x^6y^5})=4(3x^2y\sqrt[3]{2y^2})\\\\i.e.\\\\4(\sqrt[3]{54x^6y^5})=12x^2y(\sqrt[3]{2y^2})](https://img.qammunity.org/2018/formulas/mathematics/high-school/q01zbrf2xsi362exji1ikfugmm0m4z1s25.png)
( Since,
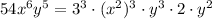 )
)
Hence, we get the simplified expression as:
![4x(\sqrt[3]{16x^3y})+12x^2y(\sqrt[3]{2y^2})=4x(\sqrt[3]{2y})+12x^2y(\sqrt[3]{2y^2})](https://img.qammunity.org/2018/formulas/mathematics/high-school/dfiwcahmpybrdmjmidbici52t3ywm44l6j.png)