Question

Solve for x, y, and z.
y=1/2z
x+2y+5z=2
3x+6y-3z=9

Answer 1

Rearrange the equation,

0x + y - ½z = 0 ==> Equation 1
x + 2y + 5z = 2 ==> Equation 2
3x + 6y - 3z = 9 ==> Equation 3

Put the 3 equation in matrix form,


`0\ \ \ \ \ 1\ \ -{(1)/(2) }\ \ \ \ \ \ \ \ 0 \\ 1\ \ \ \ \ 2\ \ \ \ \ \ \ 5\ \ =\ 2 \\ 3\ \ \ \ \ 6\ \ -3\ \ \ \ \ \ \ \ \ 9`

Find the determinant, D, of the matrix,


`0\ \ \ \ \ 1\ \ -{(1)/(2) } \\ 1\ \ \ \ \ 2\ \ \ \ \ \ \ 5\ = \ D \\ 3\ \ \ \ \ 6\ \ -3`

By Sarrus' rule,
D = [(0 × 2 × -3) + (1 × 5 × 3) + (-½ × 1 × 6)] - [(-½ × 2 × 3) + (5 × 6 × 0) + (-3 × 1 × 1)]
D = [0 + 15 + (-3)] - [(-3) + 0 + (-3)]
D = 12 + 6
D = 18

By cramer's rule,

x = Determinant of x ÷ D
Let determinant of x = Dx,


`0\ \ \ \ \ 1\ \ -{(1)/(2) } \\ 2\ \ \ \ \ 2\ \ \ \ \ \ \ 5\ = \ Dx \\ 9\ \ \ \ \ 6\ \ -3`
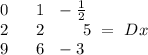
To get this determinant, substitude 0, 2 and 9 with the unknown you're finding, in this case, x.

By Sarrus' rule,
Dx = [(0 × 2 × -3) + (1 × 5 × 9) + (-½ × 2 × 6)] - [(-½ × 2 × 9) + (0 × 5 × 6) + (-3 × 1 × 2)]
Dx = [0 + 45 + (-6)] - [-9 + 0 + (-6)]
Dx = 39 + 15
Dx = 54

x = Dx ÷ D
x = 54 ÷ 18
x = 3

By cramer's rule,

y = Determinant of y ÷ D
Let determinant of y = Dy


`0\ \ \ \ \ 0\ \ -{(1)/(2) } \\ 1\ \ \ \ \ 2\ \ \ \ \ \ \ 5\ = \ Dy \\ 3\ \ \ \ \ 9\ \ -3`

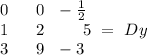
By Sarrus' rule,
Dy = [(0 × 2 × -3) + (0 × 5 × 3) + (-½ × 1 × 9)] - [(-½ × 2 × 3) + (5 × 9 × 0) + (-3 × 0 × 1)
Dy = [0 + 0 - 4½] - [-3 + 0 + 0]
Dy = -4½ + 3
Dy = -1½

y = Dy ÷ D
y = -1½ ÷ 18
y ≈ 0.0833 (3 significant figure)

Solving z using equation rule,
y = ½z
0.0833 = ½z
z = 0.0833 ÷ ½
z ≈ 0.167 (3 significant figure)

∴ x = 3, y = 0.0833 and z = 0.167.