Question

If 9 f(x) dx = 35 0 and 9 g(x) dx = 14, 0 find 9 [3f(x) + 4g(x)] dx

Answer 1

for this problem you need to know that the derivative is an associative operation, so f(x)dx+g(x)dx=[f(x)+g(x)]dx.
start by solving your two equations for f(x)dx and g(x)dx. this gets you

`9f(x)dx=350 --\ \textgreater \ f(x)dx= (350)/(9) \\ 9g(x)dx=140 --\ \textgreater \ g(x)dx= (140)/(9)`.
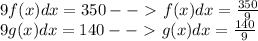
now you can change your equation you need to evaluate into something you can evaluate, using the property I explained to start.

`9[3f(x)+4g(x)]dx = 9[3(f(x)dx)+4(g(x)dx)]`.
now you know the values of f(x)dx and g(x)dx, so you can plug those in

`9[3( (350)/(9))+4((140)/(9))] \\ \\ 3(350) +4(140) \\ \\ 1610`