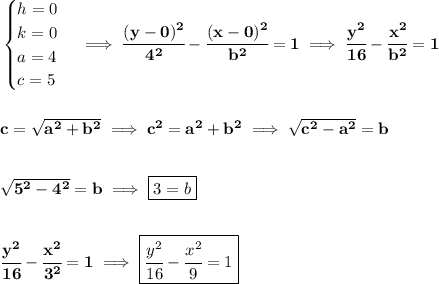Question

Write the equation of a hyperbola with vertices (0, -4) and (0, 4) and foci (0, -5) and (0, 5).

Answer 1

check the picture below. So, more or less looks like so.

notice, the center is clearly at the origin, and notice how long the "a" component is, also, bear in mind that, is opening towards the y-axis, that means the fraction with the "y" variable is the positive one.

Also notice, the "c" distance from the center to either foci, is just 5 units.


`\bf \textit{hyperbolas, vertical traverse axis }\\\\ \cfrac{(y-{{ k}})^2}{{{ a}}^2}-\cfrac{(x-{{ h}})^2}{{{ b}}^2}=1 \qquad \begin{cases} center\ ({{ h}},{{ k}})\\ vertices\ ({{ h}}, {{ k}}\pm a)\\ c=\textit{distance from}\\ \qquad \textit{center to foci}\\ \qquad \sqrt{{{ a }}^2+{{ b }}^2} \end{cases}\\\\ -------------------------------\\\\`


`\bf \begin{cases} h=0\\ k=0\\ a=4\\ c=5 \end{cases}\implies \cfrac{(y-{{ 0}})^2}{{{ 4}}^2}-\cfrac{(x-{{ 0}})^2}{{{ b}}^2}=1\implies \cfrac{y^2}{16}-\cfrac{x^2}{b^2}=1 \\\\\\ c=√(a^2+b^2)\implies c^2=a^2+b^2\implies √(c^2-a^2)=b \\\\\\ √(5^2-4^2)=b\implies \boxed{3=b} \\\\\\ \cfrac{y^2}{16}-\cfrac{x^2}{3^2}=1\implies \boxed{\cfrac{y^2}{16}-\cfrac{x^2}{9}=1}`