Question

Which of the following points is in the solution set of y < x2 - 2x - 8?

(-2, -1)(0, -2) (4, 0)

Answer 1

y < (x - 4)(x + 2)

so the critical points are -2 and 4
(-2,-1) will be in the solution

( 0,-2) will not

(4,0) will not.
the answer is ((-2,-1)

Answer 2

The correct option is 1. The point (-2,-1) is in the solution set of the given inequality.

Explanation:

The given inequality is

`y<x^2-2x-8`

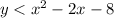
A point (x₁,y₁) is in the solution set of above inequality if the inequality satisfy by the point (x₁,y₁).

Check the inequality by (-2,-1).

Put x=-2 and y=-1 in the given inequality.

`-1<(-2)^2-2(-2)-8`

`-1<4+4-8`

`-1<0`

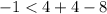
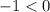
This statement is true, therefore the point (-2,-1) is in the solution set of the given inequality.

Check the inequality by (0,-2).

Put x=0 and y=-2 in the given inequality.

`-2<(0)^2-2(0)-8`

`-2<0-8`

`-2<-8`

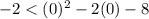
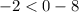
This statement is false, therefore the point (0,-2) is not in the solution set of the given inequality.

Check the inequality by (4,0).

Put x=4 and y=0 in the given inequality.

`0<(4)^2-2(4)-8`

`0<16-8-8`

`0<0`

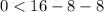
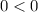
This statement is false, therefore the point (4,0) is not in the solution set of the given inequality.