Answer:
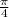
Explanation:
We have been given that the radius of a circle is 8 and the length of an arc of the circle is 2π. We are asked to find the measure of central angle subtended by the arc in radians.
We know that the arc length of a circle is equal to central angle times the radius of circle.
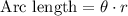
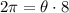
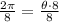
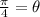
Therefore, the measure of central angle is
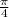 radians.
radians.