Question

Mr. Robredo is building a fence around a rectangular region with 36 feet of fencing. The area of the rectangular region is 65 square feet. What are the length and the width of the rectangular region? Enter your answers in the boxes.

Answer 1

P = 2(L + W)
P = 36
36 = 2(L + W)
36/2 = L + W
18 = L + W....L = 18 - W

A = L * W
A = 65
L = 18 - W

65 = W(18 - W)
65 = 18W - W^2
W^2 - 18W + 65 = 0
(W - 13)(W - 5) = 0

W - 13 = 0 .....L = 18 - 13
W = 13 L = 5


W - 5 = 0 L = 18 - 5
W = 5 L = 13

Not exactly sure which (length or width)...but one is 13 ft and the other is 5 ft

Answer 2

Answer: If the length of rectangle is 13 feet , then the breadth of rectangle would be 18-13=5 feet.

If the length of rectangle is 5 feet, then the breadth of rectangle would be 18-5=13 feet.

Explanation:

Since we have given that

Perimeter of rectangular region = 36 feet

Area of rectangular region = 65 sq feet

Let the length of rectangle be 'l'.

Let the breadth of rectangle be 'b'.

As we know the formula for perimeter of rectangle :

`Perimeter=2(l+b)\\\\36=2(l+b)\\\\18=l+b\\\\l=18-b`

And area of rectangle = Length × Breadth

so, it becomes

`65=b(18-b)\\\\65=18b-b^2\\\\b^2-18b+65=0\\\\b^2-13b-5b+65=0\\\\b(b-13)-5(b-13)=0\\\\(b-13)(b-5)=0\\\\b=13,5`

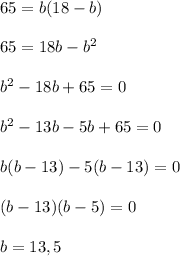
Hence, If the length of rectangle is 13 feet , then the breadth of rectangle would be 18-13=5 feet.

If the length of rectangle is 5 feet, then the breadth of rectangle would be 18-5=13 feet.