Question

Arrange the parabolas represented by the equations in increasing order with respect to the y-values of their directrixes.

Tiles
y = -x2 + 3x + 8
y = 2x2 + 15x + 18
y = x2 + 13x + 5
y = -2x2 + 4x + 8

Answer 1

y = 2x2 + 15x + 18 //With 2 being greater than 1 in 2x^2
y = x2 + 13x + 5 //Not being negative
y = -x2 + 3x + 8
y = -2x2 + 4x + 8 //Being the largest negative means it decreases the most.

Answer 2

3rd Parabola < 2nd parabola < 4th parabola < 1st parabola.

Explanation:

We are given with equation of parabolas.

We need to arrange them in increasing order with respect to y-values of their directrixes.

First we convert given equations in Standard form then find their directrix.

The standard form is (x - h)² = 4a (y - k),

then directrix is y = k - a

1). y = -x² + 3x + 8

using completing the square method,

`y=-(x^2-3x-8)`

`y=-(x^2-3x+((3)/(2))^2-8-((3)/(2))^2)`

`y=-((x-(3)/(2))^2-8-(9)/(4))`

`y=-((x-(3)/(2))^2-(41)/(4))`

`y=-(x-(3)/(2))^2+(41)/(4)`

`(x-(3)/(2))^2=-(y-(41)/(4))`

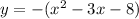
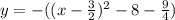
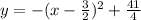
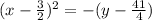
Now, by comparing with standard equation

`4a=-1\:\:\implies\:a=(-1)/(4)`

`k=(41)/(4)`

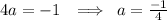
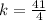
So, Directrix,
`y=(41)/(4)-(-1)/(4)=(42)/(4)=10.5`

2). y = 2x² + 15x + 18

using completing the square method,

`y=2(x^2+(15)/(2)x+9)`

`y=2(x^2+(15)/(2)x+((15)/(4))^2+9-((15)/(4))^2)`

`y=2((x+(15)/(4))^2+9-(225)/(16))`

`y=2((x+(15)/(4))^2-(81)/(16))`

`y=2(x+(15)/(4))^2-(81)/(8)`

`(x+(15)/(4))^2=(1)/(2)(y+(81)/(8))`

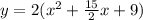
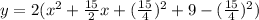
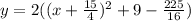
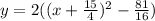
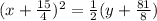
Now, by comparing with standard equation

`4a=(1)/(2)\:\:\implies\:a=(1)/(8)`

`k=(-81)/(8)`

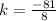
So, Directrix,
`y=(-81)/(8)-(1)/(8)=(-82)/(8)=-10.25`

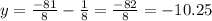
3). y = x² + 13x + 5

using completing the square method,

`y=x^2+13x+5`

`y=x^2+13x+((13)/(2))^2+5-((13)/(2))^2`

`y=(x+(13)/(2))^2+5-(169)/(4)`

`y=(x+(13)/(2))^2-(149)/(4)`

`(x+(13)/(2))^2=(y+(149)/(4))`

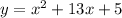
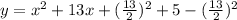
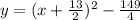
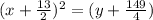
Now, by comparing with standard equation

`4a=1\:\:\implies\:a=(1)/(4)`

`k=(-149)/(4)`

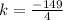
So, Directrix,
`y=(-149)/(4)-(1)/(4)=(-150)/(4)=-37.5`

4). y = -2x² + 4x + 8

using completing the square method,

`y=-2(x^2-2x-4)`

`y=-2(x^2-2x+(1)^2-4-(1)^2)`

`y=-2((x-1)^2-4-1)`

`y=-2((x-1)^2-5)`

`y=-2(x-1})^2+10`

`(x-1})^2=(-1)/(2)(y-10)`

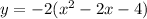
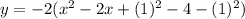
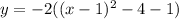
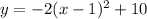
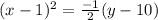
Now, by comparing with standard equation

`4a=(-1)/(2)\:\:\implies\:a=(-1)/(8)`

`k=10`

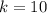
So, Directrix,
`y=10-(-1)/(8)=(81)/(8)=10.125`

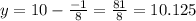
So, from above

y = 37.5 < y = -10.25 < y = 10.125 < y = 10.5

Therefore, 3rd Parabola < 2nd parabola < 4th parabola < 1st parabola.