Answer:
population in 2003 is 234 million.
Explanation:
A country's population in 1991 was 231 million
In 1999 it was 233 million.
We have to calculate the population in 2003.
Since population growth is always represented by exponential function.
It is represented by
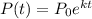
Here t is time in years, k is the growth constant, and is initial population.
For year 1991 ⇒
233 =
 = 231
= 231
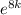
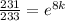
Taking ln on both the sides ⇒

ln 233 - ln 231 = 8k [since ln e = 1 ]
5.451 - 5.4424 = 8k
k =
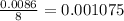
For year 2003 ⇒
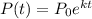
P (t) = 231 ×
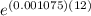
= 231 ×

= 231 × 1.0129
= 233.9 ≈ 234 million
Therefore, population in 2003 is 234 million.