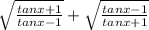Question

If tanx=(b)/(a), find the value of \sqrt((a+b)/(a-b))+\sqrt((a-b)/(a+b)) in terms of x

Answer 1

Let's find at first
`\sqrt((a+b)/(a-b))`

Let's find (a+b)(a-b)....

we should divide both side of fraction by b and we will get the following:

`( (a+b)/(b) )/( (a-b)/(b) ) \\ ( (a)/(b) + 1 )/( (a)/(b) - 1 ) \\ ( tanx + 1 )/( tanx - 1 )`

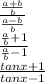
and (a-b)/(a+b) is same as (1/[(a+b)/(a-b)]) so we can use previous answer and finally we will have (a-b)/(a+b) = 1/[ (tanx + 1) / (tanx - 1)] = (tanx - 1)/(tanx + 1) and final answer will be this:


`\sqrt{ (tanx + 1)/(tanx - 1) } + \sqrt{ (tanx - 1)/(tanx + 1) }`