Answer:
 or
or
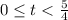
Explanation:
An acorn falls from the branch of a tree to the ground 25 feet below.
The distance, S, that the acorn is from the ground as it falls is represented by the equation
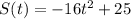
Where, t is number of seconds.
We need to find the time for which acorn moving through the air.
If acorn in air then S(t)>0

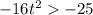
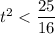
Taking square root both sides
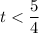
Interval of t,
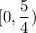
Hence, t is less than 5/4 and greater than 0.