Question

The age of a rock is determined by the function, A(t) = A 0 e -0.000002t, where Isotope Q, with an initial value of A 0, decays at a constant rate 0.000002 per year, for a number of years (also known as the age of the rock), t. A sample originally has 80 grams of Isotope Q, decays, and now has 20 grams of the isotope. Determine the current age of the sample, in years. Round your answer to the nearest thousand years. Make sure to include the correct place value commas in your answer.

Answer 1

A(t) = A 0 e -0.000002t
A (t) 20
A0. 80
T time in years?
20=80 e -0.000002t
Solve for t
20/80=e -0.000002t
Log (20/80)=log (e)×-0.000002t
T=(log(20÷80)÷log(e))÷(−0.000002)
T=693,147 years

Answer 2

The age of a rock is determined by the function:

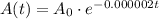`A(t) = A_0 \cdot e^(-0.000002t)` .....[1]

where,

A(t) be the age of rock after t years

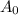`A_0` be the initial value of Isotope Q.

t be the number of years.

As per the statement:

A sample originally has 80 grams of Isotope Q, decays, and now has 20 grams of the isotope.

⇒
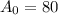`A_0 = 80` gram and A(t) = 20 grams

Substitute in [1] we have;

`20 =80 \cdot e^(-0.000002t)`

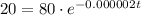
Divide both sides by 80 we have;

`0.25 = e^(0.000002t)`

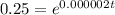
Taking ln with base e both sides we have;

`\ln 0.25 = -0.000002t`

⇒
`-1.3862943611199 = -0.000002t`

Divide both sides by 0.000002 we have;

693147.18056 = t

or

t = 693147.18056 years

Therefore, the current age of the sample, in years to the nearest thousand years is, 6,93,147 year