Question

What is the solutions of x^2 = 19x + 1

Answer 1

`x^2 = 19x + 1 \\ x^2 - 19x - 1=0 \\ D=b^2-4ac=(-19)^2-4*1*(-1)=365 \\ \\ x_(1,2)= (-bб √(D) )/(2a) \\ \\ x_(1)= (19- √(365) )/(2) \\ \\ x_(2)= (19+ √(365) )/(2)`

Answer 2

`x_(1)= =19.05\\\\x_(2)=-0.05\\`

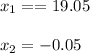
Explanation:

Hello

In elementary algebra, the quadratic formula is the solution of the quadratic equation. There are other ways to solve the quadratic equation instead of using the quadratic formula, such as factoring, completing the square, graphing and others.

let a polynom

`ax^(2) +bx+c=0`

this can be solved d by using the quadratic equation formula

`x= \frac{-bб \sqrt{b^(2)-4ac } }{2a}`

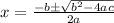
Let

`x^(2) =19x+1\`

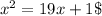
Step 1

do the equation=0

`x^(2) =19x+1\\x^(2)-19x-1=0`

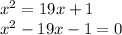
define

`a=1\\b=-19\\c=-1\\`

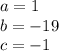
Sep two

put the values into the equation

`x= \frac{-bб \sqrt{b^(2)-4ac } }{2a}\\\\\\x= \frac{-(-19)б \sqrt{(-19)^(2)-4(1)(-1) } }{2*1}\\x= (+19б √(361+4 ) )/(2)\\x= (+19б 19.10 )/(2)\\\\x_(1)=(+19+ 19.10 )/(2) =19.05\\\\x_(2)=(+19- 19.10 )/(2) =-0.05\\\\`

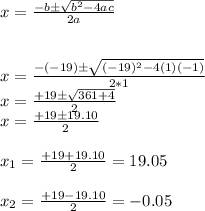
Have a good day