Question

Match each function with the corresponding restrictions to its domain when p(x)=2x and q(x) = 2^x.

Answer 1

1 = C

2 = A

3 = D

4 = B

5 = E

Alternatively, your right boxes should look like:

2

4

1

3

5

You're welcome.

Answer 2

Recall that the domain of a function is the set of all x values of the function for which the function is defined.

Given that

`p(x)=2x` and
`q(x)=2^x`


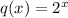
Given that

`r(x)= (q(x))/(p(x)) = (2^x)/(2x)`
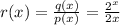
For the function to be undefined, the denominator should be zero
i.e. 2x = 0 which means that x = 0
Thus, the domain of the function is all real values of x except 0.

Therefore, the restriction is x ≠ 0.


Given that

`r(x)= (1)/(p(x)-q(x)) = (1)/(2x-2^x)`
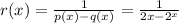
For the function to be undefined, the denominator should be zero
i.e.

`2x-2^x=0 \\ 2^x=2x`
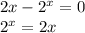
For x = 2,

`2^2 = 2(2)=4`
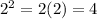
Also, for x = 1

`2^1 = 2(1)=2`
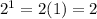
Thus, the domain of the function is all real values of x except 1 and 2.

Therefore, the restriction is x ≠ 1, 2.

Given that

`r(x)= (1)/(p(x)+16q(x))=(1)/(2x+16(2^x))`
For the function to be undefined, the denominator should be zero
i.e.

`2x+16(2^x)=0 \\ 2x+2^4(2^x)=0 \\ 2x+2^(4+x)=0`
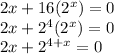
For x = -2,

`2(-2)+2^(4-2)=-4+2^2=-4+4=0`.
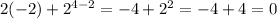
Thus, the domain of the function is all real values of x except -2.

Therefore, the restriction is x ≠ -2.


Given that

`r(x)=p(x)\circ q(x)=p(q(x))=2(2^x)`
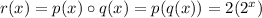
There is no value of x, for which the function is undefined.
Thus, the domain of the function is all real values of x.

Therefore, there is no restrictions to the domain of the function.


Given that

`r(x)= (q(x))/(p(x)+2)=(2^x)/(2x+2)`
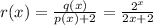
For the function to be undefined, the denominator should be zero
i.e.

`2x+2=0 \\ 2x=-2 \\ x = -1`
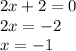
Thus, the domain of the function is all real values of x except -1.

Therefore, the restriction is x ≠ -1.